Geometry
The perimeter of kite is 172.11 cm
Explanation:
ΔABD and ΔBCD are isosceles triangles
Join the two points A and C and the let the point be O where this lines cuts BD
Given
CO = 2 × AO ( CO is height of ΔBCD, AO is height of ΔA
BD )
and
BD = 1.5 × CO
Area of Kite = Area of ΔBCD + Area of ΔABD
If the height of ΔABD = h then height of ΔBCD =2×h
DB = 1.5 × 2×h = 3×h
Area of ΔABD =
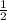 ×
×
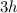 ×
×
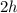
Area of ΔBCD =
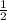 ×
×
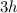 ×
×
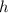
Area of Kite = 1800 = Area of ΔABD + Area of ΔBCD
1800 =
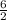 ×
×
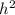 +
+
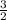 ×
×
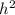 =
=
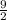 ×
×
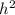
⇒
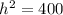
⇒ h = 20
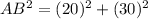
AB =
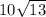 cm
cm
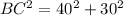
BC = 50 cm
So the perimeter of kite = AB + BC +CD +AD
⇒

⇒100 + 20
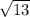
⇒172.11 cm
Hence the perimeter of kite is 172.11 cm