Answer: It has two distinct real zeros.
Explanation:
The formula that is used to calculate the discriminant of a Quadratic function is the one shown below:
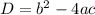
In this case you have the following Quadractic function provided in the exercise:
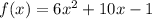
Let's make it equal to 0:
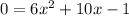
You can identify that:
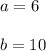
Knowing these values, you can substitute them into the formula and then evaluate:
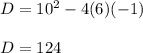
Therefore, since:
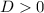
You can determine that the it has two distinct real roots.