Question

A certain practical current source provides 0.680555555555555 W to a 50 Ω load. That same practical current source provides 1.11783376314223 W to an 460 Ω load. If the same practical current source had a resistance RL is connected to it, creating a voltage across RL of vL and a current through RL of iL. Find the values of RL, vL, and iL if

(a) vL×iL is maximum
(b) vL is a maximum
(c) iL is a maximum.

(a) RL = Ω , vL = V , iL = A
(b) RL = Ω , vL = V , iL = A
(c) RL = Ω , vL = V , iL = A

Answer 1

Step-by-step explanation:

Parameters

RL = load resistance

PL = Power output to the load

IL = load current

Rs = internal resistance of the source

Is = source current

in the first condition

RL = 50 ohms, PL = 0.68055555555555

in the second case

RL = 460 ohms PL = 1.11783376314223

the diagram is as shown attached below

`I_l = I_s * (R_s)/(R_s + R_l)............1\\\\P_l = (I_l)^(2) * R_l ...................2\\\\`

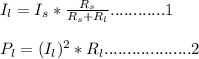
Substituting for Il in eqn 2

`P_l = (I_s)^(2) * (R_s^(2) * R_l)/((R_s + R_l)^(2) ) ............3`

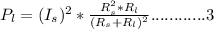
Using equation 3 for both cases

case 1

`0.68055555555555 = (I_s)^(2) * (R_s^(2) * 50)/((R_s + 50)^(2) ) ............4`

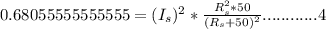
case 2

`1.11783376314223 = (I_s)^(2) * (R_s^(2) * 460)/((R_s + 460)^(2) ) ............5`

solving equation 4 and 5 we get

`I_s = 0.07063 A\\\\R_s = 39.12`

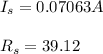
[a]

when Vl * il is maximum then

Rl = Rs

⇒ Rl = 39.12 Ohms

Using equation 1

`I_l = I_s * (R_s)/(R_s + R_l)............1\\\\I_l = 0.07064 * (39.12)/(39.12 + 39.12)\\\\I_l = 0.0353`

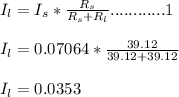
Vl = il * Rl = 0.0353 * 39.12 = 1.3817 V

hence,

IL = 0.0353 A RL = 39.12 Ohms VL= 1.38 V

[b]

When VL is maximum

VL is max when RL = ∞ (infinite)

from equation 1

IL = 0

VL = Is * Rs = 0.0764 * 39.12 = 2.763 V

[c]

when IL is a Maximum

⇒ RL = 0 ohms

substituting RL = 0 in equation 1

IL = Is = 0.0764 A

VL = IL * RL = 0.0764 * 0 = 0