Question

Suppose that the number of calls per hour to an answering service follows a Poisson process with rate 4. Suppose that 3/4's of the calls are made by men, 1/4 by women, and the sex of the caller is independent of the time of the call, (a) What is the probability that in 1 h exactly two men and three women will call the answering service? (b) What is the probability three men will make phone calls before three women do?

Answer 1

(a) The probability that in one hour exactly two men and three women will call the answering service is 0.01374.

(b) The probability that three men will make phone calls before three women do is 0.00687.

Explanation:

Let X = number of calls per hour to an answering service.

The average number of calls per hour is, λ = 4.

The random variable X follows a Poisson distribution with parameter λ = 4.

The probability mass function of X is:

`P(X=x)=(e^(-4)4^(x))/(x!);\ x=0,1,2,3...`

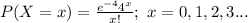
Let Y = number of calls made by a man.

The probability that a call is made by a man is,
`p=(3)/(4)`.

A randomly selected call is made by a man independently of the other calls.

Te random variable Y follows a Binomial distribution with parameters n and p.

The probability mass function of Y is:

`P(Y=y)={n\choose y}*((3)/(4))^(y)* ((1)/(4))^(n-y);\ y=0,1,2,3...`

The random variable X are independent of each other.

(a)

Compute the probability that in one hour exactly two men and three women will call the answering service as follows:

P(X = 5, Y = 2) = P (X = 5) × P (Y = 2)

`=(e^(-4)4^(5))/(5!)* [{5\choose 2}*((3)/(4))^(2)* ((1)/(4))^(5-2)]\\=0.1563* [10* 0.5625* 0.015625]\\=0.01374`

Thus, the probability that in one hour exactly two men and three women will call the answering service is 0.01374.

(b)

The random variable Z can be defined as the number of calls made by women.

The random variable Z is defined as the number of failures before a fixed number of successes (z) . That is, the number of calls made by men before a specific number of women made the calls.

The random variable Z follows a Negative Binomial distribution.

The probability mass function of Z is:

`P(Z=z)={n-1\choose z-1}* ((1)/(4))^(z)* ((3)/(4))^(n-z)`

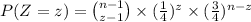
Compute the probability that three men will make phone calls before three women do as follows:

P (X = 6, Z = 3) = P (X = 6) × P (Z = 3)

`=(e^(-4)4^(6))/(6!)* [{6-1\choose 3-1}* ((1)/(4))^(3)* ((3)/(4))^(6-3)]\\=0.1042* [10* 0.015625* 0.421875]\\=0.00687`

Thus, the probability that three men will make phone calls before three women do is 0.00687.