Question

Every few years, the National Assessment of Educational Progress asks a national sample of eighth-graders to perform the same math tasks. The goal is to get an honest picture of progress in math. Suppose these are the last few national mean scores, on a scale of 0 to 500.

Year 1990 1992 1996 2000 2003 2005 2008
Score 263 268 271 272 276 277 279
(a) Find the regression line of mean score on time step-by-step. First calculate the mean and standard deviation of each variable and their correlation (use a calculator with these functions). Then find the equation of the least-squares line from these
(b) What percent of the year-to-year variation in scores is explained by the linear trend?

Answer 1

a)X: 0 2 6 10 13 15 18

Y:263 268 271 272 276 277 279

X represent the number of years since 1990

n=7
`\sum x = 64, \sum y = 1906, \sum xy= 17647, \sum x^2 =858, \sum y^2 =519164`

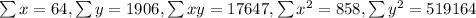
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(7(17647)-(64)(1906))/(√([7(858) -(64)^2][7(519164) -(1906)^2]))=0.97599`

`\bar X = (\sum_(i=1^n X_i))/(n) = 9.14286`

`\bar Y = (\sum_(i=1^n Y_i))/(n) = 272.286`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=858-(64^2)/(7)=272.857`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=17647-(64*1906)/(7)=220.714`

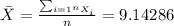
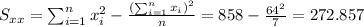
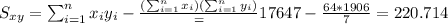
And the slope would be:

`m=(220.714)/(272.857)=0.809`

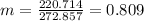
Now we can find the means for x and y like this:

And we can find the intercept using this:

`b=\bar y -m \bar x=272.286-(0.809*9.143)=264.889`

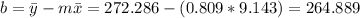
So the line would be given by:

`y=0.809 x +264.889`

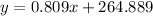
b) For this case the percent of variation in scores is explained by the linear trend is given by the determination coefficient
`r^2` and we got:

`r^2 =0.976^2 = 0.9526`

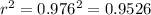
So then we can say that the percent of variation explained is approximately 95.26%

Explanation:

Pearson correlation coefficient(r), "measures a linear dependence between two variables (x and y). Its a parametric correlation test because it depends to the distribution of the data. And other assumption is that the variables x and y needs to follow a normal distribution".

Solution to the problem

Part a

We assume the following data:

X: 0 2 6 10 13 15 18

Y:263 268 271 272 276 277 279

X represent the number of years since 1990

n=7
`\sum x = 64, \sum y = 1906, \sum xy= 17647, \sum x^2 =858, \sum y^2 =519164`

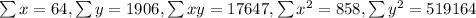
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(7(17647)-(64)(1906))/(√([7(858) -(64)^2][7(519164) -(1906)^2]))=0.97599`

So then the correlation coefficient would be r =0.976

The mean for X on this case is given by:

`\bar X = (\sum_(i=1^n X_i))/(n) = 9.14286`

`\bar Y = (\sum_(i=1^n Y_i))/(n) = 272.286`

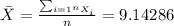
For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

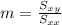
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

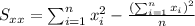
So we can find the sums like this:

`\sum_(i=1)^n x_i = 64`

`\sum_(i=1)^n y_i =1906`

`\sum_(i=1)^n x^2_i =858`

`\sum_(i=1)^n y^2_i =519164`

`\sum_(i=1)^n x_i y_i =17647`

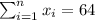
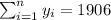
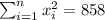
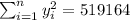
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=858-(64^2)/(7)=272.857`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=17647-(64*1906)/(7)=220.714`

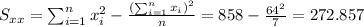
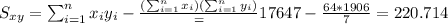
And the slope would be:

`m=(220.714)/(272.857)=0.809`

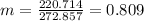
Now we can find the means for x and y like this:

And we can find the intercept using this:

`b=\bar y -m \bar x=272.286-(0.809*9.143)=264.889`

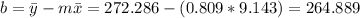
So the line would be given by:

`y=0.809 x +264.889`

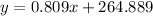
Part b

For this case the percent of variation in scores is explained by the linear trend is given by the determination coefficient
`r^2` and we got:

`r^2 =0.976^2 = 0.9526`

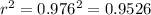
So then we can say that the percent of variation explained is approximately 95.26%