Final answer:
The price of the bonds is $17036.54.
Step-by-step explanation:
To calculate the price of the bonds, we need to use the present value formula. The formula for the present value of a bond is:
Price = (Coupon Payment /
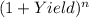 ) + (Face Value /
) + (Face Value /
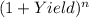 )
)
Where:
- Coupon Payment is the periodic interest payment
- Yield is the yield to maturity as a decimal
- n is the number of periods until maturity
- Face Value is the par value of the bond
In this case, the Coupon Payment is $165 ($10,000 * 3.3% / 2), the Yield is 0.038, n is 30 (15 years * 2 semiannual payments), and the Face Value is $10,000.
Plugging these values into the formula, we get:
Price = ($165 /
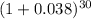 ) + ($10,000 /
) + ($10,000 /
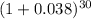 ) = $10357.78 + $6678.76 = $17036.54
) = $10357.78 + $6678.76 = $17036.54
Therefore, the price of the bonds is $17036.54.