Answer:
Magnitude of the force is 2.135N and the direction is 41.8° below negative y-axis
Step-by-step explanation:
The stiff wire 50.0cm long bent at a right angle in the middle
One section lies along the z axis and the other is along the line y=2x in the xy plane
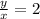
tan θ = 2
Therefore,
slope m = tan θ = y / x
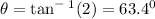
Then length of each section is 25.0cm
so, length vector of the wire is
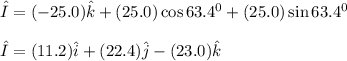
And magnetic field is B = (0.318T)i
Therefore,
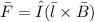
![\bar F = (20.0)[(0.112m)i +(0.224m)j-(0.250m)k * 90.318T)i]](https://img.qammunity.org/2021/formulas/physics/college/aoya156qnbnexn88mmreu1or40h8akoodn.png)
![= (20.0)(i(0)+j(-0.250)(0.318T)+k[0-(0.224m)(0.318T)]\\\\=(20.0)(-0.250)(0.318)j-(20.0)(0.224)(0.318T)\\\\=-(1.59N)j-(1.425N)k](https://img.qammunity.org/2021/formulas/physics/college/4r2lnirpl18qxknmy0zikodbrsub490tqt.png)
Magnitude of the force is
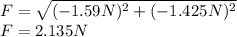
Direction is

Magnitude of the force is 2.135N and the direction is 41.8° below negative y-axis