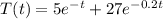Question

The rate of change of the temperature T(t) of a body is still governed by

dT
/dt
= âk(T â A), T(0) = T0,

when the ambient temperature A(t) varies with time. Suppose the body is known to have

k = 0.2

and initially is at 32°C; suppose also that

A(t) = 20eât.

Find the temperature T(t).

Answer 1

`T(t)=5e^(-t)+27e^(-0.2t)`

Explanation:

QUESTION

The rate of change of the temperature T(t) of a body is still governed by

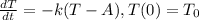`(dT)/(dt)=-k(T-A), T(0)=T_0` when the ambient temperature A(t) varies with time. Suppose the body is known to have k = 0.2 and initially is at 32°C; suppose also that
`A(t) = 20e^(-t)`. Find the temperature T(t).

SOLUTION

`(dT)/(dt)=-k(T-A), T(0)=T_0, A(t) = 20e^(-t), k=0.2`

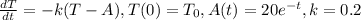
`(dT)/(dt)=-0.2T+20(0.2)e^(-t)\\(dT)/(dt)+0.2T=4e^(-t)\\\text{Integrating factor}=e^(0.2t)\\(dTe^(0.2t))/(dt)=4e^(-t)e^(0.2t)\\dTe^(0.2t)=4e^(-t)e^(0.2t)dt\\\int d[Te^(0.2t)]=4\int e^(-t(1-0.2))dt\\Te^(0.2t)=4\int e^(-0.8t)dt\\Te^(0.2t)=(4)/(-0.8) e^(-0.8t)+C, \text{C a constant of integration}\\Te^(0.2t)=-5 e^(-0.8t)+C\\T(t)=5 e^(-0.8t)e^(-0.2t)+Ce^(-0.2t)\\T(t)=5e^(-t)+Ce^(-0.2t)\\When t=0, T_0=32\\32=5+C\\C=27`

Therefore:

`T(t)=5e^(-t)+27e^(-0.2t)`