Question

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 2.4% per hour. How many hours does it take for the size of the sample to double?

Answer 1

It takes approximately 20.8 hours for the size of the bacteria sample to double.

Step-by-step explanation:

The growth rate of the bacteria population is 2.4% per hour, which means that the number of bacteria doubles every 1 / (2.4/100) = 41.67 hours. To find the number of hours it takes for the population to double, we divide 41.67 by 2, since we want to know how long it takes for the size of the sample to double. Therefore, it takes approximately 20.8 hours for the size of the sample to double.

Answer 2

It would take approximately 289 hours for the population to double

Step-by-step explanation:

Recall the expression for the continuous exponential growth of a population:

`N(t)=N_0\,e^(kt)`

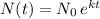
where N(t) measures the number of individuals, No is the original population, "k" is the percent rate of growth, and "t" is the time elapsed.

In our case, we don't know No (original population, but know that we want it to double in a certain elapsed "t". We also have in mind that the percent rate "k" would be expressed in mathematical form as: 0.0024 (mathematical form of the given percent growth rate).

So we need to solve for "t" in the following equation:

`2\,N_0=N_0\,e^(0.0024\,t)\\(2\,N_0)/(N_0) =e^(0.0024\,t)\\2=e^(0.0024\,t)\\ln(2)=0.0024\,t\\t=(ln(2))/(0.0024) \\t=288.811\,\, hours`

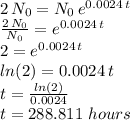
Which can be rounded to about 289 hours