Question

Two cylinders are similar. The volume of one is 64 cm^3, and the volume of the other is 729 cm^3. Find the scale factor between them.

Answer 1

4 : 9

Explanation:

`(s)/(s) =\frac{\sqrt[3]{64} }{\sqrt[3]{729} } = (4)/(9) = 4 : 9`

Answer 2

Given:

Two cylinders are similar. The volume of one is 64 cm³ and the volume of the other is 729 cm³.

We need to determine the scale factor between them.

Scale factor:

Since, it is given that the volume of two cylinders, we need to take cube root.

Thus, we have;

`Scale \ factor=64:729`

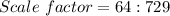
Taking cube root, we get;

`Scale \ factor=\sqrt[3]{64} :\sqrt[3]{729}`

Simplifying, we have;

`Scale \ factor=4:9`

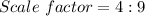
Thus, the scale factor between the two cylinders is 4 : 9