Answer:
The Growth rate constant (k) will be =
 per minute or 0.308 per hour.
per minute or 0.308 per hour.
Step-by-step explanation:
Given,
N₀ = 4596 cells / ml
N = 206104972 cells / ml
t = 15 hours
We know that,
n =
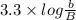
Where,
n = no. of generation during the period of exponential growth.
∴ n =
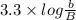
=

= 3.3 × 44844.42
∴ n = 15.350
We know that,
g =

Where,
g = generation time
t = duration of exponential growth
∴ g =
 or ∴ g =
or ∴ g =

=
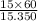 = 15 / 15.350
= 15 / 15.350
= 900 / 15.350 ∴ g = 0.977 hours
∴ g = 58.63 minutes
We know that,
k =

Where, k = specific growth rate
∴ k =
 or ∴ k =
or ∴ k =

= 0.301 / 58.63 = 0.301 / 0.977
∴ k =
 per minutes ∴ k = 0.308 per hour
per minutes ∴ k = 0.308 per hour