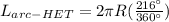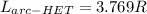Question

Using the image, determine the length of each arc.

THE
degrees
MGIF =
degrees
MHET
degrees

Answer 1

`GIF=1.239 R`

`HET= 3.769 R`

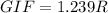
Explanation:

Assuming the image is the shown below, we can use the following formula to find the length of arc
`L_(arc)`:

`L_(arc)=2 \pi R ((\theta)/(360 \°))`

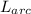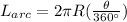
Where
`\theta` is the angle in the arc and
`R` is the radius of the circle.

Since we are not given the value of
`R`, we will only work with this.

For
`GIF`:

`L_(arc-GIF)=2 \pi R ((71\°)/(360 \°))`

`L_(arc-GIF)=1.239 R`

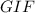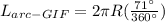
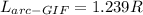
For
`HET`:

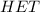We firstly need to find the value of this angle, taking into account the whole circumference is
`360 \°`:

`360 \°=71 \°+53 \°+HET+20 \°`

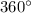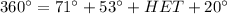
Finding
`HET`:

`HET=216 \°`

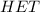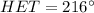
Now, let's calculate the length of arc:

`L_(arc-HET)=2 \pi R ((216\°)/(360 \°))`

`L_(arc-HET)=3.769 R`