Answer:
a)
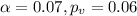
Since
 we "reject" the null hypothesis
we "reject" the null hypothesis
b)
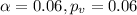
Since
 we "reject" the null hypothesis
we "reject" the null hypothesis
c)
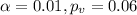
Since
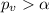 we " do not reject" the null hypothesis
we " do not reject" the null hypothesis
Explanation:
Some previous concepts
The p-value is the probability of obtaining the observed results of a test, assuming that the null hypothesis is correct.
The null hypothesis attempts "to show that no variation exists between variables or that a single variable is no different than its mean"
The alternative hypothesis "is the hypothesis used in hypothesis testing that is contrary to the null hypothesis"
For any hypotehsis test we reject the null hypothesis is:

In the other case we FAIL to reject the null hypothesis when:
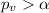
Solution to the problem
Part a
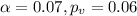
Since
 we "reject" the null hypothesis
we "reject" the null hypothesis
Part b
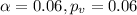
Since
 we "reject" the null hypothesis
we "reject" the null hypothesis
Part c
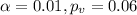
Since
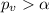 we " do not reject" the null hypothesis
we " do not reject" the null hypothesis