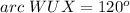Question

What is the measure of WUX in Circle V ?

Answer 1

`arc\ WUX=120^o`

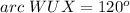
Explanation:

The complete question is:

In circle V, angle WXZ measures 30°. Line segments WV, XV, ZV, and YV are radii of circle V. Circle V is shown. Line segments W V, X V, Z V, and Y V are radii. Lines are drawn from point W to point X and from point Z to point Y to form secants. Point U is on the circle between points W and X. What is the measure of Arc W U X in circle V?

The picture of the question in the attached figure

step 1

Find the measure of angle XWV

we know that

The triangle VWX is an isosceles triangle, because has two equal sides (VX=VW)

we have

`m\angle WXZ=30^o\\m\angle WXV=m\angle WXZ`

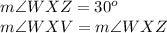
so

`m\angle WXV=30^o`

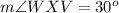
Remember that an isosceles triangle has two equal interior angles

so

step 2

Find the measure of angle WVX

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

`m\angle\ WVX+m\angle XWV+m\angle WXV=180^o`

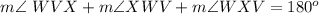
substitute the given values

`m\angle WVX+30^o+30^o=180^o\\m\angle WVX=180^o-60^o=120^o`

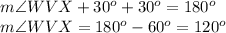
step 3

Find the measure of arc WUX

we know that

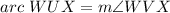`arc\ WUX=m\angle WVX` ----> by central angle

we have

`m\angle WVX=120^o`

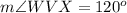
therefore

`arc\ WUX=120^o`