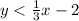Question

Write the slope-intercept inequality for the graph below?

Answer 1

Given:

Given that the graph of the inequality.

We need to determine the equation of the inequality.

Slope:

Let us substitute the coordinates (3,-1) and (-3,-3) in the slope formula, we get;

`m=(-3+1)/(-3-3)`

`m=(-2)/(-6)`

`m=(1)/(3)`

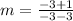
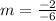
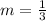
Thus, the slope of the inequality is
`m=(1)/(3)`

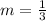
Equation of the line:

The equation of the line can be determined using the formula,

`y-y_1=m(x-x_1)`

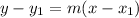
Substituting the point (3,-1) and the slope
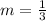`m=(1)/(3)`, we get;

`y+1=(1)/(3)(x-3)`

`y+1=(1)/(3)x-1`

`y=(1)/(3)x-2`

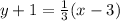
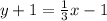
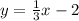
Thus, the equation of the line is
`y=(1)/(3)x-2`

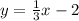
Equation of the inequality:

From the graph, it is obvious that the line of the graph is a dashed line then inequality is either < or >

Thus, the inequality of the equation must be either
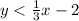`y<(1)/(3)x-2` or
`y>(1)/(3)x-2`

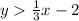
Since, the shaded portion of the graph contains the point (0,0), we need to determine the inequality that contains the point.

Hence, substituting (0,0) in the inequality
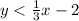`y<(1)/(3)x-2`, we get;

`0<(1)/(3)(0)-2`

`0<2`

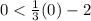
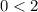
Thus, the coordinate (0,0) satisfies the condition, then the inequality of the given graph is
`y<(1)/(3)x-2`

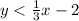
Hence, the inequality of the graph is
`y<(1)/(3)x-2`