Question

Giulia is designing glass storage jars with surface area 675 cm2.The jars are cylinders. She wants to maximize the volume of each jar to save on the materials cost. a) What dimensions should Giulia use? b) What will the volume be?

Answer 1

a) radius: 6.0 cm, height: 11.9 cm

b)
`1345.9 cm^3`

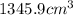
Explanation:

a)

The surface area of a cylinder is given by the sum of:

- The area of the two bases, so
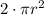`2\cdot \pi r^2`, where r is the radius of the cylinder

- The lateral area of the cylinder, so
`2\pi r h`, where h is the height of the cylinder

So the surface area can be written as

`A=2\pi r^2 + 2\pi r h`

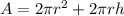
Re-arranging the equation, we can rewrite it making h the subject:

`2\pi r h=A-2\pi r^2\\h=(A)/(2\pi r)-r` (1)

The volume of the cylinder instead is given by

`V=\pi r^2 h`

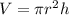
By substituting (1) into this expression, we find:

`V=\pi r^2 ((A)/(2\pi r)-r)=(Ar)/(2)-\pi r^3`

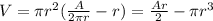
Here we want to maximize the volume of the jar, so we have to require its first derivative to be zero, so:

`(dV)/(dr)=0\\(A)/(2)-3\pi r^2 = 0\\r=\sqrt{(A)/(6\pi)}`

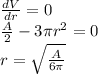
We also know that the surface area of the jar must be

`A=675 cm^2`

So, the radius of the cylinder must be

`r=\sqrt{(675)/(6\pi)}=6.0 cm`

While the height is

`h=(A)/(2\pi r)-r=(675)/(2\pi (6.0))-6.0=11.9 cm`

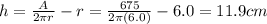
b)

The volume of the cylinder is given by:

`V=\pi r^2 h`

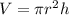
where

r is the radius of the cylinder

h is the height of the cylinder

In this problem, we have:

r = 6.0 cm is the radius of the jar

h = 11.9 cm is the height of the jar

So, the volume of the jar is

`V=\pi (6.0)^2 (11.9)=1345.9 cm^3`