Answer:
original fraction = 1/6
Explanation:
Since the denominator is greater than the numerator by 5, then the fraction should be:
x/x+5.
Again, if 3 is added to the numerator and 2 added to the denominator, then the fraction is increased by 1/3.
This means -
x+3/x+5+2
= x+3/x+7
As it is now, the fraction is already increased by one third of the original fraction.
That is:

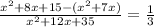
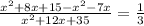
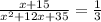
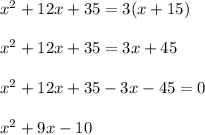
we then factorize
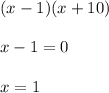
we will then substitute x for 1 in the fraction
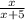
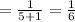
This is the original fraction.