Question

Light of wavelength 600 nm passes though two slits separated by 0.25 mm and is observed on a screen 1.4 m behind the slits. The location of the central maximum is marked on the screen and labeled y = 0.

At what distance, on either side of y = 0, are the m = 1 bright fringes ?

Answer 1

y = 3.36 mm

Step-by-step explanation:

The wavelength of the light,
`\lambda = 600 nm= 600 * 10^(-9) m`

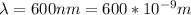
Separation between the two slits, d = 0.25 mm

`d = 0.25 * 10^(-3) m`

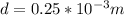
The separation between the light image and the screen, L = 1.4 m

m = 1

the distance of the bright fringes from the central maximum,
`y = (m \lambda L)/(d)`

`y = (1 * 600 * 10^(-9) )/(0.25 * 10^(-3) )`

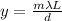
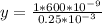
y = 0.00336 m

y = 3.36 mm

Answer 2

y(m=+1,-1)=3.36mm

Step-by-step explanation:

We have to take into account the expression for the position of the fringes

`y=(m\lambda D)/(d)`

Where lambda is the wavelength of the light, D is the distance to the screen, m is the order of the fringe and d is the distance between slits.

By replacing we have

`y=((1)(600*10^(-9)m)(1.4m))/(0.25*10^(-3)m)=3.36*10^(-3)m`

There is a distance of 3.36mm to the secon maximum in the screen.

HOPE THIS HELPS!!