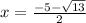Given:
The quadratic equation is

We need to determine the solutions of the quadratic equation.
Solution:
Let us solve the equation to determine the value of x.
Adding both sides of the equation by 5x and 3, we get;
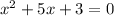
The solution of the equation can be determined using quadratic formula.
Thus, we get;
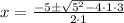
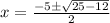
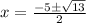
Thus, the two roots of the equation are
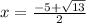 and
and
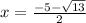
Hence, the solutions of the equation are
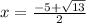 and
and