Question

Find the maximum profit and number of units that must be produced and sold in order to yield max profit. Assume revenue, R(x) and cost C(x) are in dollars:

R(x) = 50x-.1x^2 and C(x) = 6x+30

Answer 1

One needs to sell 220 units of the product to earn a maximum profit of $4,870.

Explanation:

The revenue is
`R(x)=50x-0.1x^2`.

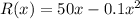The cost is
`C(x)=6x+30`

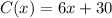
The profit is given by,

Profit = Revenue - Cost

`P(x)=50x-0.1x^2-(6x+30)`

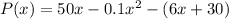
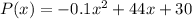`P(x)=-0.1x^2+44x+30` ....(1)

To maximize the above profit function in (1) we find its critical points.

`P'(x)=-0.2x+44`

`-0.2x+44=0`

`x=(44)/(0.2)`

`x=220`

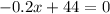
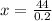
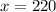
To verify this critical point is a point of maximum, we calculate the second derivative of P(x) to get

`P''(x)=-0.2<0`

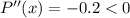
Hence from the second derivative test, x = 220 is a point of maximum for P(x).

Substitute x in profit,

`P(220)=-0.1(220)^2+44(220)+30`

`P(220)=4870`

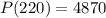
One needs to sell 220 units of the product to earn a maximum profit of $4,870.