Question

What is the volume of grain that could completely fill this silo, rounded to the nearest whole number? Use 22 over 7 for pi. (4 points) Group of answer choices 13,750 ft3 14,012 ft3 262 ft3 4,583 ft3

Answer 1

19,461 ft

Explanation:

Answer 2

Answer:
`19,461\ ft^3`

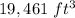
Explanation:

The missing figure is attached.

The volume of grain that could completely fill this silo is the sum of the volume of the cylinder and the volume of the hemisphere.

By definition, the volume of a cylinder can be calculated with this formula:

`V_c=\pi r^2h`

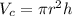
Where "r" is the radius and "h" is the height.

In this case you know that:

`r=6\ ft\\\\h=168\ ft`

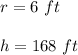
And the volume of a hemisphere can be found using the following formula:

`V_h=(2)/(3) \pi r^3`

Where "r" is the radius.

In this case:

`r=6\ ft`

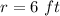
Therefore, the volume of grain that could completely fill this silo, rounded to the nearest whole number, is:

`V_(grain)=((22)/(7))(6\ ft)^2 (168\ ft)+(2)/(3) ((22)/(7))(6\ ft)^3\\\\V_(grain)\approx19,461\ ft^3`