Question

Which is the graph of the linear inequality y ≥ −x − 3?

On a coordinate plane, a solid straight line has a negative slope and goes through (negative 3, 0) and (0, negative 3). Everything to the right of the line is shaded.
On a coordinate plane, a solid straight line has a negative slope and goes through (negative 3, 0) and (0, negative 3). Everything to the left of the line is shaded.
On a coordinate plane, a dashed straight line has a negative slope and goes through (negative 3, 0) and (0, negative 3). Everything to the right of the line is shaded.
On a coordinate plane, a dashed straight line has a negative slope and goes through (negative 3, 0) and (0, negative 3). Everything to the left of the line is shaded.

Answer 1

A

Explanation:

edge 23

Answer 2

Given:

The given inequality is
`y \geq-x-3`

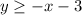
We need to determine the graph of the linear inequality.

Slope:

From the given inequality, the slope of the line is given by

`m=-1`

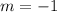
Thus, the slope of the inequality is -1.

x and y intercept:

The x - intercept can be determined by substituting y = 0 in the equation.

Thus, we have;

`0=-x-3`

`x=-3`

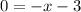
Thus the coordinates of the x - intercept is (-3,0)

The y - intercept can be determined by substituting x = 0 in the equation.

Thus, we have;

`y =-0-3`

`y=-3`

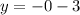
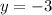
Thus, the coordinate of the y - intercept is (0,-3)

Graphing the inequality:

Let us substitute the coordinate (0,0) to determine the shaded portion.

Thus, we get;

`0\geq -0-3`

`0\geq -3`

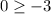
Thus, the coordinate satisfies the inequality.

Hence, the everything to the right of the line is shaded.

Also, the symbol "≥" denotes the solid line.

Thus, On a coordinate plane, a solid straight line has a negative slope and goes through (negative 3, 0) and (0, negative 3). Everything to the right of the line is shaded.

Hence Option A is the correct answer.