Answer:
a)
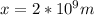 and
and
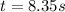
b) t = γt', so it is 8.35 s.
Step-by-step explanation:
a) The equation of Lorentz transformations is given by:
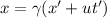
x' and t' are the position and time in the moving system of reference, and u is the speed of the space ship. x is related to the observer reference.
- x' = 0
- t' = 5.00 s
- u =0.800 c, c is the speed of light 3*10⁸ m/s
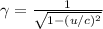
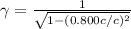
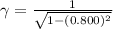
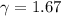
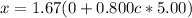
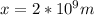
Now, to find t we apply the same analysis:
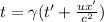
but as x'=0 we just have:
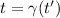
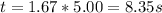
b) Here, Mavis reads 5 s on her watch and Stanley measured the events at a time affected by the Lorentz factor, in other words t = γt', if we see it is the same a) part. So the time interval will be equal to 8.35 s.
I hope it helps you!