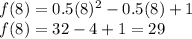Question

The first three terms of a sequence are 1, 2, and 4. Susanna said the 8th term of this sequence is 128. Paul said the 8th term is 29. Explain how the students found their answers. Why could these both be considered correct answers?

Answer 1

Sussanna considered the sequence to be geometric while Paul considered it to be quadratic.

Explanation:

The first three terms of a sequence are 1, 2, and 4.

Sussanna considered this sequence as a geometric sequence with first term a=1 and common ratio r=2.

The 8th term of this sequence is given by:

`= a {r}^(7)`

`= 1 * {2}^(7)`

`= 1 * 128`

`= 128`

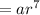
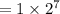
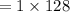
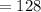
Paul considered the sequence to be quadratic.

Paul obtained the equation follow:

`a( {1)}^(2) + b(1) + c = 1 \\ a + b + c = 1....(1)`

`a( {2)}^(2) + b(2) + c = 1 \\ 4a +2 b + c = 2....(2)`

`a( {3)}^(2) + b(3) + c = 4\\ 9a + 3b + c = 4....(3)`

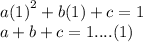
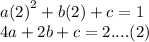
He solved the three equations simultaneously to get:

`a = 0.5 \\ b = - 0.5 \\ c = 1`

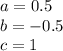
He then obtain the rule;

`f(n) = 0.5 {n}^(2) - 0.5n + 1`

To find the 8th term, he substitute n=8.

`f(8) = 0.5( {8})^(2) - 0.5(8)+ 1 \\ f(8) = 32 - 4 + 1 = 29`