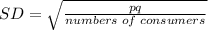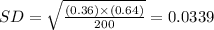Question

An investment website can tell what devices are used to access the site. The site managers wonder whether they should enhance the facilities for trading via smartphones so they want to estimate the proportion of users who access the site that way (even if they also use their computers sometimes) . They draw a random sample of 200 investors from their customers. Suppose that the true proportion of smartphone users is 36%. a) What would you expect the shape of the sampling distribution for the sample proportion to be? b) What would be the mean of this sampling distribution? c) What would be the standard deviation of the sampling distribution?

Answer 1

The following are the answers given below.

a)- normal

b)- 0.36

c)- 0.03369

Step-by-step explanation:

a)- The sampling distribution pattern to the proportion of the sample should be normal because test proportions nearer to the following should become more probable, as well as the test proportions further beyond the following in any way might be increasingly fewer possible.

In certain terms, that form of the distribution of the test ratio is supposed to bulge in the midst as well as a taper at the end, so that would become somewhat normal.

b)- The mean of such a sample distribution should become identical for the actual 36% of the following users.

Consequently, p=0.36

c)- Given:

p=0.36

`q=1-p`

`q=1-0.36`
`=0.64`

`There\;are\;200\;consumers`

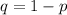
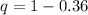
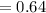
So, let the standard deviation should be SD.

`SD=\sqrt{(pq)/(numbers\;of\;consumers) }`

`SD=\sqrt{((0.36)*(0.64))/(200) } = 0.0339`