Question

Speakers A and B are vibrating in phase. They are directly facing each other, are 8.0 m apart, and are each playing a 75.0-Hz tone. The speed of sound is 343 m/s. On the line between the speakers there are three points where constructive interference occurs. What are the distances of these three points from speaker A?

Answer 1

The distances of the three points from speaker A is 1). 1.713 m, 2). 4 m,

3). 6.287 m.

Step-by-step explanation:

Here we have

Speed of sound, v = fλ

Where:

f = Frequency of sound and

λ = Wavelength of the sound

Therefore, λ = v/f =
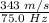`\frac{343 \hspace{0.09cm}m/s}{75.0 \hspace{0.09cm}Hz}` = 4.573 m

The two speakers are 8.0 m apart

Let X be a point from speaker A on the line where we have constructive interference. Therefore,

(L - X) - X = n·λ

Which gives
`X= (L - n\cdot \lambda)/(2)`

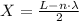
Therefore, we have, when n = 0,

`X= (8 - 0\cdot 4.573)/(2) = 4 m`

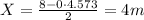
When n = 1 we have

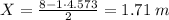`X= (8 - 1\cdot 4.573)/(2) = 1.71 \hspace {0.09cm} m`, which is the distance from speaker A, since from the nature of the calculation, if we selected X to be from speaker B, then there will be a point of constructive interference at 1.71 m from speaker B

In other words since there is a point of constructive interference at the mid point, we will have constructive interference at λ/2 on either side of the mid point

Therefore, the three points are;

4 - (4.573 m)/2, 4, 4+(4.573 m)

The distances of the three points from speaker A is

1). 1.713 m,

2). 4 m,

3). 6.287 m.

Answer 2

4 m, 1.71 m and 6.29 m

Step-by-step explanation:

Let L = 8 m be the distance between the two speakers. Let x be the distance from speaker A of constructive interference. The distance to speaker B from the point of constructive interference is thus x₁ = L - x.

There is constructive interference when the distance x₁ - x = nλ where n = is an integer and λ = wavelength L - x

x₁ - x = nλ

L - x - x = nλ

L - 2x = nλ

x = (L - nλ)/2 = (L - nv/f)/2. where v = speed of wave = 343 m/s and f = frequency = 75 Hz

The distance from A where constructive interference would occur starts from when

n = 0

x₂ = (L - nv/f)/2 = (8 - 0 × 343/75)/2 = (8 - 0)/2 = 8/2 = 4 m

n = 1

x₃ = (L - nv/f)/2 = (8 - 1 × 343/75)/2 = (8 - 4.57)/2 = 3.43/2 = 1.71 m

when n = 2

x₄ = (L - nv/f)/2 = (8 - 2 × 343/75)/2 = (8 - 9.14)/2 = -1.15/2 = -0.57 m

So the value at n = 2 is not included.

The third point occurs at x₅ = L - x₃ where x₃ = 1.71 m is the distance away from point B where constructive interference also occurs. (since it is symmetrical about the point x₂ = 4 m

x₅ = L - x₃ = 8 - 1.71 = 6.29 m