Question

Lagrange multipliers have a definite meaning in load balancing for electric network problems. Consider the generators that can output xi megawatts, i = 1, 2, 3 each generator cost

Ci = 3xi + ( i /40) xi^2 i .

If the total power needed is 1000MW. What load balance (x1, x2, x3) minimizes cost?

Answer 1

The load balance
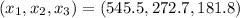`(x_1,x_2,x_3)=(545.5,272.7,181.8)` Mw minimizes the total cost

Explanation:

Optimizing With Lagrange Multipliers

When a multivariable function f is to be maximized or minimized, the Lagrange multipliers method is a pretty common and easy tool to apply when the restrictions are in the form of equalities.

Consider three generators that can output xi megawatts, with i ranging from 1 to 3. The set of unknown variables is x1, x2, x3.

The cost of each generator is given by the formula

`\displaystyle C_i=3x_i+(i)/(40)x_i^2`

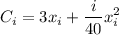
It means the cost for each generator is expanded as

`\displaystyle C_1=3x_1+(1)/(40)x_1^2`

`\displaystyle C_2=3x_2+(2)/(40)x_2^2`

`\displaystyle C_3=3x_3+(3)/(40)x_3^2`

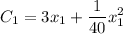
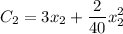
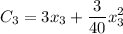
The total cost of production is

`\displaystyle C(x_1,x_2,x_3)=3x_1+(1)/(40)x_1^2+3x_2+(2)/(40)x_2^2+3x_3+(3)/(40)x_3^2`

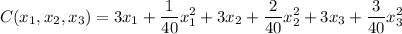
Simplifying and rearranging, we have the objective function to minimize:

`\displaystyle C(x_1,x_2,x_3)=3(x_1+x_2+x_3)+(1)/(40)(x_1^2+2x_2^2+3x_3^2)`

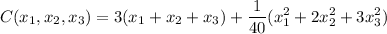
The restriction can be modeled as a function g(x)=0:

`g: x_1+x_2+x_3=1000`

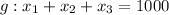
Or

`g(x_1,x_2,x_3)= x_1+x_2+x_3-1000`

We now construct the auxiliary function

`f(x_1,x_2,x_3)=C(x_1,x_2,x_3)-\lambda g(x_1,x_2,x_3)`

`\displaystyle f(x_1,x_2,x_3)=3(x_1+x_2+x_3)+(1)/(40)(x_1^2+2x_2^2+3x_3^2)-\lambda (x_1+x_2+x_3-1000)`

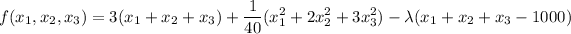
We find all the partial derivatives of f and equate them to 0

`\displaystyle f_(x1)=3+(2)/(40)x_1-\lambda=0`

`\displaystyle f_(x2)=3+(4)/(40)x_2-\lambda=0`

`\displaystyle f_(x3)=3+(6)/(40)x_3-\lambda=0`

`f_\lambda=x_1+x_2+x_3-1000=0`

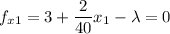
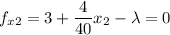
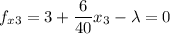
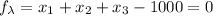
Solving for \lambda in the three first equations, we have

`\displaystyle \lambda=3+(2)/(40)x_1`

`\displaystyle \lambda=3+(4)/(40)x_2`

`\displaystyle \lambda=3+(6)/(40)x_3`

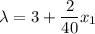
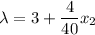
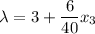
Equating them, we find:

`x_1=3x_3`

`\displaystyle x_2=(3)/(2)x_3`

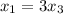
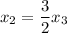
Replacing into the restriction (or the fourth derivative)

`x_1+x_2+x_3-1000=0`

`\displaystyle 3x_3+(3)/(2)x_3+x_3-1000=0`

`\displaystyle (11)/(2)x_3=1000`

`x_3=181.8\ MW`

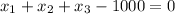
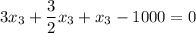
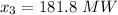
And also

`x_1=545.5\ MW`

`x_2=272.7\ MW`

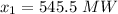
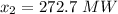
The load balance
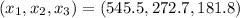`(x_1,x_2,x_3)=(545.5,272.7,181.8)` Mw minimizes the total cost