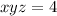Question

Given that (x+y+z)(xy+xz+yz)=18 and that x^2(y+z)+y^2(x+z)+z^2(x+y)=6 for real numbers x, y, and z, what is the value of xyz?

Answer 1

4

Explanation:

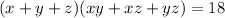`(x+y+z)(xy+xz+yz)=18` Equation 1

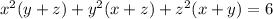`x^2(y+z)+y^2(x+z)+z^2(x+y)=6` Equation 2

What is the value of
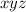`xyz` where each variable represents a real number?

Let's expand equation 1:

`(x+y+z)(xy+xz+yz)=18`

`x(xy)+x(xz)+x(yz)+y(xy)+y(xz)+y(yz)+z(xy)+z(xz)+z(yz)=18`

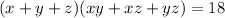
Simplify each term if can:

`x^2y+x^2z+xyz+y^2x+xyz+y^2z+xyz+z^2x+z^2y=18`

See if we can factor a little to get some of the left hand side of equation 2:

The first two terms have
`x^2` and if I factored
`x^2` from first two terms I would have
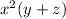`x^2(y+z)` which is the first term of left hand side of equation 2.

So let's see what happens if we gather the terms together that have the same variable squared together.

`x^2y+x^2z+y^2x+y^2z+z^2y+z^2x+xyz+xyz+xyz=18`

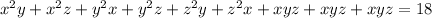
Factor the variable squared terms out of each binomial pairing:

`x^2(y+z)+y^2(x+z)+z^2(y+x)+xyz+xyz+xyz=18`

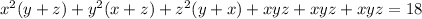
Replace the sum of those first three terms with what it equals which is 6 from the equation 2:

`6+xyz+xyz+xyz=18`

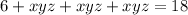
Combine like terms:

`6+3xyz=18`

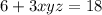
Subtract 6 on both sides:

`3xyz=12`

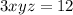
Divide both sides by 3:

`xyz=4`