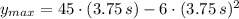Answer:
a)
![\vec r (t) = \left[(90\cdot \cos \theta)\cdot t \right]\cdot i + \left[(90\cdot \sin \theta)\cdot t -6\cdot t^(2) \right]\cdot j](https://img.qammunity.org/2021/formulas/mathematics/college/fcw1m8gnz2aojjuja93g4vhxo3ibcqv5op.png) , b)
, b)
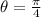 , c)
, c)
 ,
,
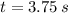 .
.
Explanation:
a) The function in terms of time and the inital angle measured from the horizontal is:
![\vec r (t) = [(v_(o)\cdot \cos \theta)\cdot t]\cdot i + \left[(v_(o)\cdot \sin \theta)\cdot t -(1)/(2)\cdot g \cdot t^(2) \right]\cdot j](https://img.qammunity.org/2021/formulas/mathematics/college/7ua1theds980ye7csw6kz3eyhij56ntjhn.png)
The particular expression for the cannonball is:
![\vec r (t) = \left[(90\cdot \cos \theta)\cdot t \right]\cdot i + \left[(90\cdot \sin \theta)\cdot t -6\cdot t^(2) \right]\cdot j](https://img.qammunity.org/2021/formulas/mathematics/college/fcw1m8gnz2aojjuja93g4vhxo3ibcqv5op.png)
b) The components of the position of the cannonball before hitting the ground is:
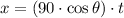
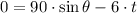
After a quick substitution and some algebraic and trigonometric handling, the following expression is found:
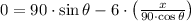

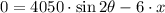
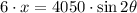

The angle for a maximum horizontal distance is determined by deriving the function, equalizing the resulting formula to zero and finding the angle:
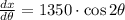
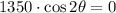
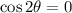
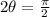
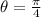
Now, it is required to demonstrate that critical point leads to a maximum. The second derivative is:
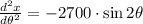
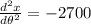
Which demonstrates the existence of the maximum associated with the critical point found before.
c) The equation for the vertical component of position is:
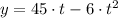
The maximum height can be found by deriving the previous expression, which is equalized to zero and critical values are found afterwards:
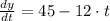
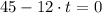
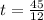
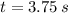
Now, the second derivative is used to check if such solution leads to a maximum:
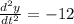
Which demonstrates the assumption.
The maximum height reached by the cannonball is: