Question

A quadrilateral has two angles that measure 222° and 81°. The other two angles are in a ratio of 6:13. What are the measures of those two angles?

Answer 1

`\sf\huge\underline{\star Solution:-}`

`\rightarrow` Ratio of two angles are 6:13.

So, let the one angle be
`\sf{6x}` and another be
`\sf{13x.}`

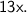
As we know that,

Sum of all interior angles of a quadrilateral =
`\sf\pink{360°.}`

So let's sum up the given angles,

`\rightarrow`
`\sf{222°+81°+6x+13x \:=\: 360°}`

`\rightarrow`
`\sf{303+19x \:=\: 360°}`

`\rightarrow`
`\sf{19x \:=\: 360-303}`

`\rightarrow`
`\sf{19x \:=\: 57}`

`\rightarrow`
`\sf{x \:=\: (19)/(57)}`

`\rightarrow`
`\sf{x \:=\: 3}`

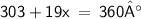
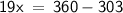
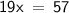
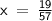
Hence,
`\sf{x \:=\: 3}`

So, First angle
`\sf{= \:6x\: = \:6×3 \:=}`
`\sf\purple{18°.}`

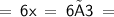
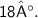
Second angle
`\sf{= \:13x\: = \:13×3 \:=}`
`\sf\purple{39°.}`

_________________________________

Hope it helps you:)