Question

Participants saw a series of words on a computer screen. Each time, a word (either relating to a positive emotion or a negative emotion) was presented on a screen for 1500ms. Researchers asked participants to press the "A" key as quickly as possibly if they saw a positive word and the "L" key if they saw a negative word. The response is reaction time in milliseconds (i.e., how long it took the subject to make a response).

Subjects Positive Negative
1 500 490
2 540 540
3 340 350
4 540 580
5 480 500
6 465 490
7 400 450
8 440 450
9 430 420
10 435 450
Questions:
1. Identify the independent variable and its associated levels, as well as the dependent variable.
2. Identify the statistical test to be used.
3. State the null and alternative hypothesis.
4. Determine the critical value(s).
5. Calculate the value of your test statistic from the data.
6. Draw a distribution showing your critical regions and test statistic.
7. Make a statistical decision for the hypotheses.
8. Interpret the results and answer/validate the research question - Did the reaction time differ between the two types of words?

Answer 1

1) The independent variable is the type of word that has two possible values: positive / negative.

The dependant variable is the time of reaction of the subjects.

2) T-student test of the difference of two means, with estimated standard deviation.

3)

`H_0: \mu_p-\mu_n=0\\\\H_a: \mu_p-\mu_n\\eq0`

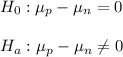
4) The critical values are t_c=±1.734.

5) t=-0.53

6) Attached

7) The null hypothesis failed to be rejected.

8) There is no enough evidence to claim that the reaction time differ between the two types of words.

Explanation:

2) In this case, the statistical test is an hypothesis test comparing both means, to know if the time of reaction to positive words is different from the time of reaction to negative words.

As we will work with sample standard deviation as a estimation of the population standard deviation, we will use a T-student test.

3) The null and alternative hypothesis are:

`H_0: \mu_p-\mu_n=0\\\\H_a: \mu_p-\mu_n\\eq0`

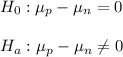
4) The critical values depend on the number of degrees of freedom and the level of significance. Assuming a significance level of α=0.10 and having 18 degrees of freedom,

`df=n_p+n_p-2=10+10-2=18`

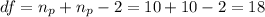
the critical values are t_c=±1.734.

5) The sample mean and standard deviation for the Positive words reaction time is:

`M_p=457\\\\s_p=62`

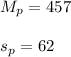
The sample mean and standard deviation for the Negative words reaction time is:

`M_n=472\\\\s_n=64`

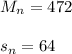
The estimation of the standard deviation of the difference is:

`s_d=\sqrt{(s_p^2+s_n^2)/(n) }=\sqrt{(62^2+64^2)/(10) }=√(794) =28.2`

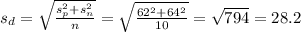
Then, the t-statistic can be calculated as:

`t=((M_p-M_n)-(\mu_p-\mu_n))/(\s_d)=((457-472)-0)/(28.17)=(-15)/(28.17)= -0.53`

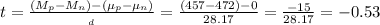
6) Attached

t= t-statistical

tc: t-critical

7) The t-statistic lies in the acceptance region, so the null hypothesis failed to be rejected.

8) There is no enough evidence to claim that the mean time of reaction to positive words is different from the mean time of reaction to negative words.