Question

Which angle does not appear to have a measure of 23 degrees?

Answer 1

Correct option: H

Step-by-step explanation:

In each case we have a protractor and two rays that meet at the center of the protractor. So let's call the α the angle between the two rays, then if in one case
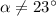`\alpha \\eq 23^(\circ)`, the that angle will not appear to have a measure of 23 degrees. In order to solve this problem let's check each case:

Case F.

The first ray lies on angle
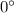`0^(\circ)` while the second ray lies on angle
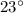`23^(\circ)`. Then:

`\alpha=23^(\circ)-0^(\circ)=23^(\circ)`

This angle measures 23 degrees.

Case G.

The first ray lies on angle
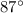`87^(\circ)` while the second ray lies on angle
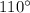`110^(\circ)`. Then:

`\alpha=110^(\circ)-87^(\circ)=23^(\circ)`

This angle measures 23 degrees.

Case H.

The first ray lies on angle
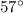`57^(\circ)` while the second ray lies on angle
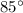`85^(\circ)`. Then:

`\alpha=85^(\circ)-57^(\circ)=28^(\circ)`

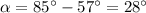
This angle doesn't measure 23 degrees.

Case J.

The first ray lies on angle
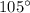`105^(\circ)` while the second ray lies on angle
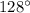`128^(\circ)`. Then:

`\alpha=128^(\circ)-105^(\circ)=23^(\circ)`

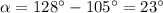
This angle measures 23 degrees.

Conclusion: The angle that will not appear to have a measure of 23 degrees is the one for case H.