Question

Which graph correctly compares the volumes, V, of rectangular pyramids with different heights, h, when their bases all have the dimensions of 4 feet by 6 feet? (Recall that the volume of a rectangular pyramid can be found using the formula, V = one-third B h, where V is the volume, B is the area of the base, and h is the height.)

Answer 1

The graph that has

(1,8) and (2,16)

Step-by-step explanation:

i took the test

Answer 2

• A coordinate plane with a line that passes through the points (1,8), (2,16), (3,24), (4,32), (5,40), and others that can be found given different values to h in the equation V = 8h.

Step-by-step explanation:

1. Volume of a rectangular pyramid (given):

`V=(1)/(3)Base* h`

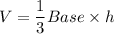
2. Base:

`4feet* 6feet=24feet^2`

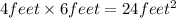
3. Volume of the rectangular pyramids with base area equal to 24 feet²:

`V=(1)/(3)* 24feet^2* h\\\\\\V=8* h=8h`

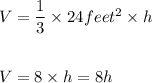
4. Table

To draw the graph you can build a table

Height in feet Volume if feet³

1 8×1 = 8

2 8×2 = 16

3 8×3 = 24

4 8×4 = 32

5 8×5 = 40

Hence, the correct graph will be a coordinate plane with a line that passes through the points (1,8), (2,16), (3,24), (4,32), (5,40), and others that can be found given different values to h in the equation V = 8h.