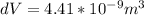Answer:
The resulting decrease in the volume is
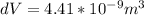
Step-by-step explanation:
The volume of the sphere is mathematically represented as

Substituting 1.2cm =
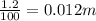 for radius
for radius
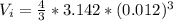
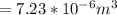
Let denote the change in volume as
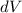
Bulk Modulus is mathematically is mathematically represented as
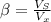
Where
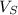 is the volumetric stress and it is mathematically evaluated as
is the volumetric stress and it is mathematically evaluated as
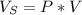
substituting
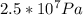 for P and
for P and
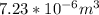 for V
for V
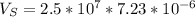

And
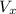 is the volumetric strain and it is mathematically evaluated as
is the volumetric strain and it is mathematically evaluated as
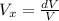
So substituting this for
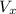 into the Bulk Modulus equation and substituting values
into the Bulk Modulus equation and substituting values
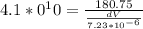
Making dV the subject