Question

The path of a baseball, hit 3 feet above ground, is modeled by the function f(x)=-0.01x^2+x+3, where f(x) represents the vertical height of the bar and X is the horizontal distance. How far across the field, in feet, of the ball travel before hitting the ground? Round to two decimal places

Answer 1

Therefore the ball travel 102.92 feet horizontally before hitting the ground

Explanation:

Given that, the path of a baseball, hit 3 feet above ground, is modeled by the function

`f(x)=-0.01 x^2+x+3`

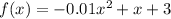
where f(x) represents the vertical height of the ball in feet(Assume) and x is the horizontal distance in feet(Assume) .

When the ball hits the ground, then the vertically distance of the ball will be zero, i.e f(x)=0

`\therefore -0.01 x^2+x+3=0`

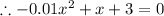
[Applying quadratic formula
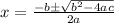`x=(-b\pm√(b^2-4ac))/(2a)` , here a = -0.001, b=1 and c=3]

`\Rightarrow x=(-1\pm√(1^2-4.(-0.01).3))/(2.(-0.01))`

`\Rightarrow x=-2.94, 102.92`

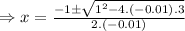
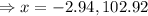
Therefore the ball travel 102.92 feet horizontally before hitting the ground.