Question

At a college production of a​ play, 420 tickets were sold. The ticket prices were​ $8, $10, and​ $12, and the total income from ticket sales was ​$3900. How many tickets of each type were sold if the combined number of​ $8 and​ $10 tickets sold was 5 times the number of​ $12 tickets​ sold?

Answer 1

There were 220 tickets of $8, 130 tickets of $10 and 70 tickets of $12 were sold.

Explanation:

Given,

Total number of tickets sold = 420

Total money collected = $3900

We need to find the number of each type of ticket.

Solution,

Let the number of $8 ticket be 'x'.

Also let the number of $10 ticket be 'y'.

And also let the number of $12 ticket be 'z'.

So the total number of tickets is equal to the sum of the number each type of ticket.

framing in equation form, we get;

`x+y+z=420\ \ \ \ \ equation\ 1`

Also given the combined number of​ $8 and​ $10 tickets sold was 5 times the number of​ $12 tickets​ sold.

So we can frame it as;

`x+y=5z\ \ \ \ equation\ 2`

Now substituting the value of equation 2 in equation 1, we get;

`5z+z=420\\\\6z=420`

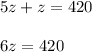
On dividing both side by '6' using division property, we get;

`(6z)/(6)=(420)/(6)\\\\z=70`

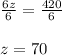
Now we get from equation 1;

`x+y+z=420\\\\x+y+70=420\\\\x+y=420-70`

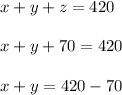
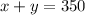`x+y=350` ⇒ equation 3

Also we can say that;

Total money collected is equal to 8 multiplied by number of $8 ticket plus 10 multiplied by number of $10 ticket plus 12 multiplied by number of $12 ticket.

framing in equation form we get;

`8x+10y+12z=3900`

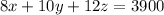
Now we will substitute value of z in above equation we get;

`8x+10y+12*70=3900\\\\8x+10y+840=3900\\\\8x+10y=3900-840\\\\8x+10y = 3060`

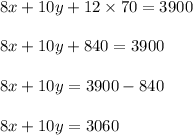
Now Dividing by 10 we get;

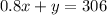`0.8x+y=306` ⇒ equation 4

subtracting equation 4 from equation 3 we get;

`x+y-(0.8x+y)=350-306\\\\x+y-0.8x-y=44\\\\0.2x=44`

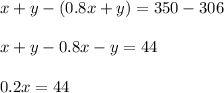
Dividing both side by 0.2 we get;

`(0.2x)/(0.2)=(44)/(0.2)\\\\x=220`

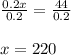
Now substituting the value of x in equation 3 we get.

`x+y=350\\\\220+y=350\\\\y=350-220\\\\y= 130`

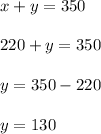
Hence There were 220 tickets of $8, 130 tickets of $10 and 70 tickets of $12 were sold.