Question

Consider this composite figure.

Marcin applied the formula for the volume of a sphere
to find the volume of the half sphere.
1. V = 743
2. V =
764
4 cm
3. V
256
I cm3
What is the next step Marcin should perform?
What is the volume of the half sphere?
V= cm3

Answer 1

a. Marcin should divide the volume of the sphere by 2.

b.
`V_(h.sphere)=128\pi cm^3`

Explanation:

The complete exercise is: "Marcin applied the formula for the volume of a sphere to find the volume of the half sphere:

`V=(4)/(3) \pi r^3\\\\V=(4)/(3) \pi (64\ cm)^3\\\\V=256\pi \ cm^3`

What is the next step Marcin should perform? What is the volume of the half sphere?

In order to solve this exercise it is important to analize the information given in the exercise.

a. You know that formula that is used to calculate the volume of a sphere is the shown below:

`V_(sphere)=(4)/(3) \pi r^3`

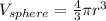
Where "r" is the radius of the sphere.

Based on the data given in the exercise, the radius is:

`r=64\ cm`

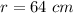
So, substiting values and evaluating, Marcin get that the volume of the sphere is:

`V_(sphere)=256\pi \ cm^3`

Then, since he needs to find the volume of a the half sphere, Marcin should divide the volume of the sphere by 2.

b. Applying that procedure, Marcin will get that the volume of the half sphere is the following:

`V_(h.sphere)=(V_(sphere))/(2)\\\\V_(h.sphere)=(256\pi cm^3)/(2)\\\\V_(h.sphere)=128\pi cm^3`