Answer: 12) y = 2x² - 7x - 4
13) y = x²
14) y = x² + 3x + 1
15) 8, 9
Explanation:
12)
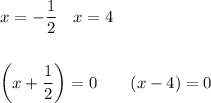
(2x + 1) = 0 (x - 4) = 0
(2x + 1)(x - 4) = 0
2x² - 7x - 4 = 0
y = 2x² - 7x - 4
13) x = 0 x = 0
(x)(x) = 0
x² = 0
y = x²
14) It is factorable if the sum of two factors of the c-value is the b-value.
One example: x² + 3x + 1 = 0
The only factors of 1 are 1 × 1 → 1 + 1 ≠ 3
So this is not factorable.
15) Let n represent one of the integers, then n + 1 is the other integer.
n(n + 1) = 72
n² + n = 72
n² + n - 72 = 0
(n - 8)(n + 9) = 0
n = 8, n = -9
Since the requirement is that the integer is positive, then n = -9 is not valid.
If n = 8, then n + 1 = 9
Answer: 8, 9