Question

A single loop of wire with an area of 0.0900m2 is in a uniform magnetic field that has an initial value of 3.80 T, is perpendicular to the plane of the loop, and is decreasing at a constant rate of 0.190 T/s. (a) What emf is induced in this loop? (b) If the loop has a resistance of 0.600Ω, find the current induced in the loop.

Answer 1

The induced loop in coil is 0.0171 V and induced current in the loop is 0.0284 A

Step-by-step explanation:

Given:

Area of loop
`A = 0.090`
`m^(2)`

Initial magnetic field
`B = 3.80` T

Rate of magnetic field
`(dB)/(dt) = 0.190`
`(T)/(s)`

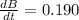
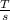
(a)

From the formula of faraday's law,

Induced emf is given by,

`\epsilon =- (d\phi)/(dt)`

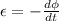
Where
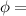`\phi =` magnetic flux

`\phi = BA`

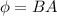
Put the value of
`\phi` in above equation,

`\epsilon = A(dB)/(dt)`

`\epsilon = 0.090 * 0.190`

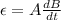
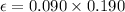
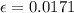`\epsilon = 0.0171` V

(b)

Resistance
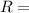`R =` 0.600Ω

The induced current in the loop is given by,

`\epsilon = IR`

`I = (\epsilon)/(R)`

`I = (0.0171)/(0.600)`

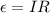
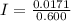
`I = 0.0284` A

Therefore, the induced loop in coil is 0.0171 V and induced current in the loop is 0.0284 A