Question

Amy works for a company that produces plastic lids and cups for restaurants. She wants to estimate what proportion of lids produced in a day have a defect that makes them not fit the cups. She takes a random sample of 250 250250 lids from the more than 10 , 000 total lids produced that day and finds 15 lids in the sample with this defect. Based on this sample, calculate the 99% confidence interval for the proportion of lids produced that day with this defect?

Answer 1

(0.021,0.099)

Explanation:

khan

Answer 2

99% confidence interval for the proportion of lids produced that day with this defect somewhere between ( .0213 , .0987) or between
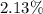`2.13\%` to
`9.87\%`

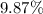
Explanation:

Given -

Sample size ( n) = 250

Sample proportion
`(\widehat{p})` =
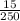`(15)/(250)` = .06

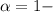`\alpha = 1 -` confidence interval = 1 - .99 = .01

`z_{(\alpha)/(2)}` =
`z_{(.01)/(2)}` = 2.58

99% confidence interval for the proportion of lids produced that day with this defect =
`\widehat{p} \pm z_{(\alpha)/(2)} \sqrt{\frac{(\widehat{p}) (1 - \widehat{p}) }{n}}`

=
`.06 \pm z_{(.01)/(2)} \sqrt{((.06) (1 - .06) )/(250)}`

=
`.06 \pm 2.58* .0150`

=
`.06 \pm .0387`

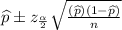
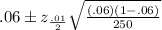
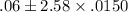
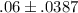
= ( .06 + .0387 ) , ( .06 - .0387 )

= ( .0987 , .0213 )