Answer:
t =0.06s and t=9.94 s
Explanation:
The equation that models the height of the rocket is
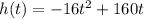
when the rocket is at height of 9 fret above the ground, then

This implies that:
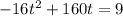
Rewrite in standard quadratic form.
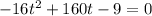
The solution is given by

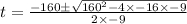
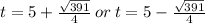
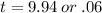
The rocket reach the height of 9 feet at times t=0.06s and t=9.94 seconds