Question

Two cylindrical swimming pools are being filled simultaneously at the same rate. The smaller pool has a radius of 5 m, and the water level rises at a rate of 0.5m/min. The larger pool has a radius of 8 m. How fast is the water level rising in the larger pool?

Answer 1

0.195m/min

Explanation:

The radii of the smaller pool =5m

The radii of the larger pool = 8m

DEFINITION:

Given two similar shapes, and the ratio of lengths in the two similar shapes, the ratio of the areas is a square of the ratio of the lengths.

The radii of the pools have a ratio of 5:8

Therefore, the ratio of surface areas will be
`5^2 : 8^2=25:64`

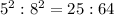
Since the pools are being filled at the same rate

Let the Volume of the Smaller Pool,
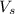`V_s` and the height of the water be
`H_s`

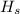
Let the Volume of the Larger Pool,
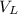`V_L` and the height of the water be
`H_L`

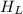
Volume of a cylinder = Base surface area X Height

`V_s=25H_s`

`V_L=64H_L`

`(dV_s)/(dt) =25(dH_s)/(dt) \\(dV_L)/(dt) =64(dH_L)/(dt) \\(dV_s)/(dt)=(dV_L)/(dt) \text{ Since the water inflow is the same rate}\\25(dH_s)/(dt)=64(dH_L)/(dt)\\(dH_s)/(dt)=0.5 m/min`

`25X0.5=64(dH_L)/(dt)\\12.5=64(dH_L)/(dt)\\(dH_L)/(dt)=(12.5)/(64)=0.195m/min`

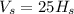
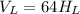
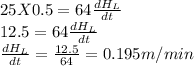
The water level is rising in the larger pool at a rate of 0.195m/min