Question

The surface of an elastic body is loaded by a uniform stress of 2000 psf over an area 30 ft by 60 ft, which has coordinates (0, 0) at the center.

Find:
(a) the vertical stress at a depth of 10 ft below a corner of the loaded area.
(b) the vertical stress at a depth of 20 ft below the center of the loaded area.
(c) the vertical stress at a depth of 30 ft below a point which has coordinates 10 ft greater than those of the corner of the loaded area in the first quadrant (first quadrant is the one with positive x and y coordinates).

Answer 1

q = 1.11 lb

`\triangle \sigma _v = 1.66 * 10^(-5)` psf

`\triangle \sigma _v = 1.66 * 10^(-5)` psf

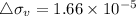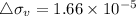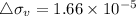`\triangle \sigma _v = 1.66 * 10^(-5)` psf

Step-by-step explanation:

given data

uniform stress = 2000 psf

area = 30 ft by 60 ft

solution

we get here surface load uniform homogenous soil is express as

q =
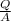`(Q)/(A)` ................1

q =
`(2000)/(30* 60)`

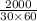
q = 1.11 lb

and

now we apply here boussin vertical stress that is at depth 10 ft

`\triangle \sigma _v` =
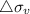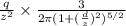`(q)/(z^2) * (3)/(2\pi (1+((d)/(z))^2)^(5/2))` ................2

`\triangle \sigma _v = (1.1)/(10^2) * (3)/(2\pi (1+((30)/(10))^2)^(5/2))`

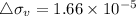`\triangle \sigma _v = 1.66 * 10^(-5)` psf

and

depth at 20 ft will be put value in equation 2

`\triangle \sigma _v = (1.1)/(20^2) * (3)/(2\pi (1+((0)/(20))^2)^(5/2))`

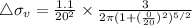
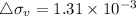`\triangle \sigma _v = 1.31 * 10^(-3)` psf

and

at depth at 30 ft

depth at 20 ft will be put value in equation 2

`\triangle \sigma _v = (1.1)/(30^2) * (3)/(2\pi (1+((30+10)/(30))^2)^(5/2))`

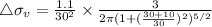
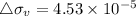`\triangle \sigma _v = 4.53 * 10^(-5)` psf