Question

Ryan drew a cylinder and a cone with identical bases and heights. Which of the following is true?

Show your work!!
20 points

Answer 1

The volume of the cylinder is three times the volume of the cone.

Explanation:

Answer 2

Answer: B. The volume of the cylinder is three times the volume of the cone.

Explanation:

The missing options are:

A. The volumes are the same.

B. The volume of the cylinder is three times the volume of the cone.

C. The volume of the cone is three times the volume of the cylinder.

D The volume of the cylinder is four-thirds the volume of the cone.

For this exercise it is important to remember the formula to find the volume of a cylinder. This is:

`V_(cylinder)=\pi r^2h`

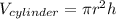
Where "r" is the radius and "h" is the height of the cylinder.

Now you must remember that the formula that is used to calculate the volume of a cone is the following:

`V_(cone)=(1)/(3) \pi r^2h`

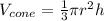
Where "r" is the radius and "h" is the height of the cone.

As you can notice:

- If a cylinder and a cone have identical bases and heights and you know the volume of the cylider, you can find the volume of the cone by multiplying the volume of the cylinder by
`(1)/(3)`

- If a cylinder and a cone have identical bases and heights and you know the volume of the cone, you can find the volume of the cylinder by multiplying the volume of the cone by 3.

Therefore, you can conclude that: The volume of the cylinder is three times the volume of the cone.