Question

Josiah has a mass of 75kgand wants to know how many helium-filled balloons it would take to fly. The density of helium is about 1kg/m^3 less than regular air, which means a cubic meter of helium can lift about 1kg. Fully inflated, a balloon has a diameter of 0.3m and can be modeled as a sphere. He neglects the mass of the balloon in his calculations. nHow mnay balloons would it take to lift a person of 75 kg mass?

Answer 1

a person with 75 kg mass will need 4762 ballons

Step-by-step explanation:

The expression for the required number of balloons is

`N = (m)/(((4)/(3)\pi r^3) ) (p_(air)-p_(he))`

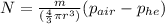
substitute 1.293kg/m^3 for density of air

0.179kg/m^3 for density of helium

75kg for mass m

radius = diameter / 2

= 0.3m / 2

= 0.15m

`N = (75)/(((4)/(3) \pi r^3)(P_(air)-P_(he)))`

`N = (75)/((4)/(3)\pi (0.15)^3(1.293-0.179) )`

`N = (75)/(1.33\pi (3.375* 10^-^3)(1.114))`

`N = (75)/(4.178(3.375* 10^-^3)(1.114)) \\\\N = 4762ballons`

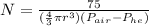
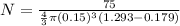
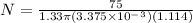
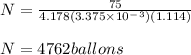
Hence, a person with 75 kg mass will need 4762 ballons

Answer 2

`n =26786\,ballons`

Step-by-step explanation:

According to the Archimedes' Principle, the buoyant force exerted on the helium ballons is equal to the weight of displaced air. A simplified scheme for the system person-ballons is presented below. The correspondent equation of equilibrium is:

`\Sigma F = \rho_(Air)\cdot V_(net)\cdot g - \rho_(He)\cdot V_(net)\cdot g - m_(person)\cdot g = 0`

`(\rho_(Air)-\rho_(He))\cdot V_(net) - m_(person) = 0`

The minimum net volume is:

`V_(net) = (m_(person))/(\rho_(Air)-\rho_(He))`

`V_(net) = (75\,kg)/(1.2\,(kg)/(m^(3))-1\,(kg)/(m^(3)) )`

`V_(net) = 375\,m^(3)`

The volume of each ballon is:

`V_(ballon) = (4)/(3)\pi\cdot (0.15\,m)^(3)`

`V_(ballon) \approx 0.014\,m^(3)`

The minimum quantity of ballons needed to lift Josiah is:

`n = (V_(net))/(V_(ballon))`

`n = (375\,m^(3))/(0.014\,m^(3))`

`n =26786\,ballons`