Question

The distribution of weights of potato chip bags filled off a production line is unknown. However, the mean is m=13.35 OZs and the standard deviation is s=.1200 OZs. To check the quality of the potato chip bags, a random sample of n=36 bags is selected. Use `X to denote the sample mean.

1. The mean (or expected value) of the sample mean `X is:______

a. 13.23
b. 13.00
c. 13.47
d. 13.50

2. The standard deviation of the sample mean `X is

a. 0.0200
b. 0.1200
c. 0.0600
d. 0.3600
e. none of the above

3. The probability that the sample mean `X is less than or equal to 13.38 OZs is closest to

a. 0.0668
b. 0.0998
c. 0.4332
d. 0.9332
e. none of the above

4. The probability that the sample mean `X is less than or equal to 13.32 OZs is closest to

a. 0.0668
b. 0.0998
c. 0.4332
d. 0.9332
e. none of the above

5. The probability that the sample mean `X is between 13.30 and 13.36 OZs is closest to

a. 0.0062
b. 0.3085
c. 0.6853
d. 0.4938
e. none of the above

Answer 1

(1) The mean (or expected value) of the sample mean `X = 13.35

(2) The standard deviation of the sample mean `X = .02

(3) The probability that the sample mean `X is less than or equal to 13.38 OZ = .9332

(4) The probability that the sample mean `X is less than or equal to 13.32 OZ = .0668

(5) The probability that the sample mean `X is between 13.30 and 13.36 OZ = .6853

Explanation:

mean
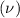`(\\u)` =13.35

Standard deviation
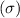`(\sigma )` = .1200

n = 36

The mean (or expected value) of the sample mean `X

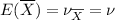`E(\overline{X}) = \\u _{\overline{X}} = \\u` = 13.35

The standard deviation of the sample mean `X =

`\sigma _{\overline{X}} = (\sigma)/(√(n))` =
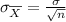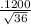`(.1200)/(√(36))` = .02

The probability that the sample mean `X is less than or equal to 13.38 OZ=

`P(\overline{X} \leq 13.38 )` =
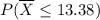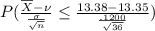`P(\frac{\overline{X} - \\u }{(\sigma)/(√(n))}\leq (13.38 - 13.35 )/((.1200)/(√(36))))` [ Z =
`\frac{\overline{X} - \\u }{(\sigma)/(√(n))}` ]

=
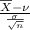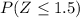`P(Z\leq 1.5)` Using Z table

= .9332

. The probability that the sample mean `X is less than or equal to 13.32 OZ =

`P(\overline{X} \leq 13.32)` =
`P(\frac{\overline{X} - \\u }{(\sigma)/(√(n))}\leq (13.32 - 13.35 )/((.1200)/(√(36))))`

=
`P(Z\leq -1.5)`

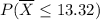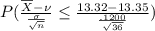
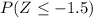
= .0668

The probability that the sample mean `X is between 13.30 and 13.36 OZ =

`P(13.30\leq \overline{X} \leq 13.36)` =
`P((13.30 - 13.35 )/((.1200)/(√(36))))\leq \frac{\overline{X} - \\u }{(\sigma)/(√(n))}\leq (13.36 - 13.35 )/((.1200)/(√(36))))`

=
`P(- 2.5\leq Z\leq 0.5)`

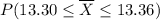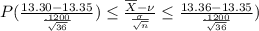
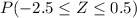
= .6915 - .0062

= .6853