Question

Find the area of this isosceles triangle.
Pythagoras’ theorem

Answer 1

120 cm²

Explanation:

The area (A) of a triangle is calculated as

A =
`(1)/(2)` bh ( b is the base and h the height )

We require to calculate h

The segment from the vertex to the base is a perpendicular bisector.

This divides the triangle into 2 right triangles, with legs 8 and h and hypotenuse 17.

Using Pythagoras' identity on the left right triangle

The square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is

h² + 8² = 17²

h² + 64 = 289 ( subtract 64 from both sides )

h² = 225 ( take the square root of both sides )

h =
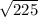`√(225)` = 15, thus

A = 0.5 × 16 × 15 = 8 × 15 = 120 cm²

Answer 2

Explanation:

first you have to divide 16/2 so you can do pythagorus to solve for the height.

16/2=8

√17^2-8^2=15cm - by adding the root symbol we can skip a step.

1/2x16x15=120cm^2