Question

Tom, Larry, Roberta, and John enjoy roller Coasters. Whenever a new roller Coaster opens near their town,

they try to be among the first to ride.
One Saturday, the four friends decide to ride a new coaster. While waiting in line, Fred notices that where
the ride begins the coaster resembles the graph of a polynomial function that they have been studying in
their Algebra 2 class.
1) The first drop of the roller coaster can be represented by the equation h(t) = t3 - 12t2 + 35t wheret is
the time in seconds and h is the height in feet. [F.IF.4,7C]
a) What is the degree of the function?
b) According to the degree of the function, how many times should the roller coaster hit the ground?
c) Will the roller coaster be in the form of a linear, quadratic, cubic or quartic graph?
Explain how you know this.

Answer 1

• a) degree 3

• b) 3 times

• c) cubic

Step-by-step explanation:

The function that represents the first drop of the roller coaster is:

`h(t)=t^3-12t^2+35t`,

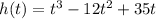where t is the time in seconds and h is the height in feet.

a) What is the degree of the function?

The degree of a polynomial is the highest power of the variable, t. Thus, the degree of the function is 3.

b) According to the degree of the function, how many times should the roller coaster hit the ground?

The number of complex roots of a polynomial is equal to the degree of the polynomial. Thus, in this case this polynomial has 3 roots. Each root represents the value of the polynomial that makes it equal to zero, this is:

`t^3-12t^2+35t=0`

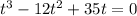
Thus, since the polynomial function represents the height of the, the value zero represents when the roller coaster hits the ground.

To learn if the three roots are real numbers you can solve the equation, which may be done by factoring the polynomial.

Take t out as common factor:

• t(t² - 12t + 35)

Find two numbers that add up -12 and its product is 35. Those are -7 and -5. Hence, use the factors t - 12 and t - 5:

• t ( t - 12) (t - 5) = 0 This is the factored form of the polynomial

Whose solutions are t =0, t = 12, and t = 5. Three real numbers.

Hence, the roller coaster hits the ground three times: first at start, then at 5 seconds, and finally at 12 seconds.

c) Will the roller coaster be in the form of a linear, quadratic, cubic or quartic graph?

It will be in the form of a cubic graph, becasue a linear graph corresponds to a polynomial of degree 1, a quadratic graph corresponds to a polynomial of degree 2, a cubic graph corresponds to a polynomial of degree 3, and a quartic graph corresponds to a polynomial of degree 4.