Question

You are at the controls of a particle accelerator, sending a beam of 1.80 x 10^7 m/s protons (mass m) at a gas target of an unknown element. Your detector tells you that some protons bounce straight back after a collision with one of the nuclei of the unknown element. All such protons rebound with a speed of 1.50 x 10^7 m/s . Assume that the initial speed of the target nucleus is negligible and the collision is elastic.

(a) Find the mass of one of the nuclei of the unknown element. Express you answer in terms of the proton mass m.
(b) What is the speed of the unknown nucleus immediately after such a collision?

Answer 1

11m

3000000 m/s

Step-by-step explanation:

`m_1` = Mass of proton

`m_2` = Mass of unknown element

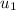`u_1` = Velocity of proton =
`1.8* 10^7\ m/s`

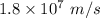
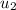`u_2` = Velocity of rebound =
`1.5* 10^7\ m/s`

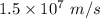
As the energy of the system is conserved we have

`m_2=(u_1-v_1)/(u_1+v_1)m_1\\\Rightarrow m_2=(1.8* 10^7-(-1.5* 10^7))/(1.8* 10^7+(-1.5* 10^7))* m_1\\\Rightarrow m_2=11m_1`

Mass of the unknown element is 11m

As the momentum of the system is conserved

`m_1u_1=m_1v_1+m_2v_2\\\Rightarrow v_2=(m_1(u_1-v_1))/(m_2)\\\Rightarrow v_2=(m_1(1.8* 10^7-(-1.5* 10^7)))/(11m_1)\\\Rightarrow v_2=3000000\ m/s`

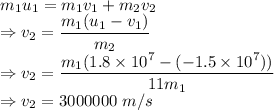
The speed of the unknown nucleus immediately after such a collision is 3000000 m/s