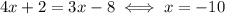The trick is to express everything in terms of powers of 3 (since both 9 and 81 are powers of 3):
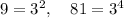
So, the equation becomes
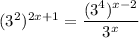
Apply the power rule
 to get
to get
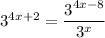
And finally the rule
 to get
to get
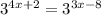
Now we get to the simple part: two powers of the same base are equal if and only if the exponents equal each other: